Yard Space #MPM1D/#MFM1P #PrBL

I took the typical “find the largest area given a specific perimeter” problem and created a hands-on, problem-based learning task for my combined grade 9 Math class (academic & applied combined):

Scenario:

Ms. Wheeler wants to build a fenced in yard for Sally to run around in.
She buys 16 1-metre long sections of fence.

What do you wonder?

Physical & Visual Representations:

The yard must be fully enclosed. Use toothpicks to create show different ways of placing the 16 pieces of fencing (I forgot to take photos of this part but they made stuff like this):

Draw your shape & label its dimensions:

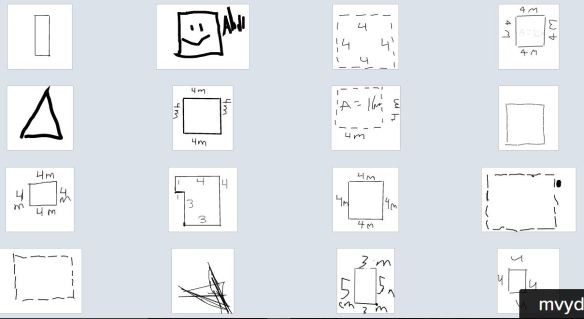
How should the pieces be set up to create the largest enclosed area possible?

What shape offers the largest area?

We discussed that while a square was the largest rectangle possible, there were other shapes possible with greater areas.

How should the pieces be set up to create the largest enclosed area possible if Ms. Wheeler uses a wall of the house as one side of the enclosure?

We have some more exploration to do here. I left this pretty open and they explored various shapes. But I’m not sure they’ve drawn any solid conclusions just yet for the case where we have 1 side of the shape already accounted for.

Get the Pear Deck slideshow here.

– Laura Wheeler (Teacher @ Ridgemont High School, OCDSB; Ottawa, ON)

Toothpick Triangles #MFM2P #3ActMath

Back at the beginning of this month we explored Dan Meyer’s toothpick triangles task:

Act 1

What do you notice?

What Mathematical questions can we ask & solve?

The question I chose for us to investigate (decided ahead of time to meet the curriculum learning goal for that day):

Act 2

Groups were given toothpicks to play with & this image with the number of toothpicks (250) in the jar displayed:

It’s important to give students enough toothpicks to extend the pattern seen in the video, but not as many as 250. My goal is for them to model mathematically, which they won’t do if they can complete the physical model w/ the manipulatives given.

I have also found lately that my students prefer to draw their model on their boards, rather than use the physical manipulatives. Perhaps I should have them work for 2 minutes with the physical manipulatives first before sending them to the boards? Thoughts?

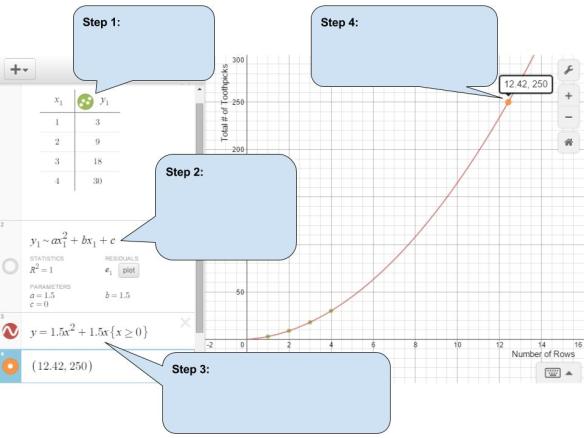
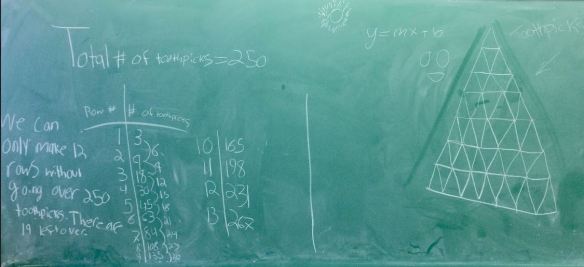The solutions from each group:You can see that they all used a table of values with second differences to continue the pattern & find an answer.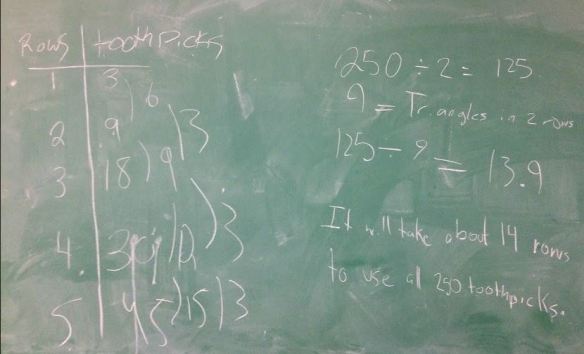 These 2 groups were trying to use some calculations but the top group could not explain to me their reason (within the context of the toothpick triangles) for dividing the total number of toothpicks by 2.
The bottom group was trying some linear proportional reasoning and using the idea of 3 toothpicks per triangle in their calculations. They didn’t make the connection between their constant second difference meaning that linear reasoning wouldn’t work here.

Act 3

The answer:The video version (which we watched) is here.

Even though our curriculum doesn’t require students to determine a quadratic equation from a table of values, it does expect them to graph the data (and I like them to use Desmos to perform a regression & find the equation since Desmos makes it so easy!). 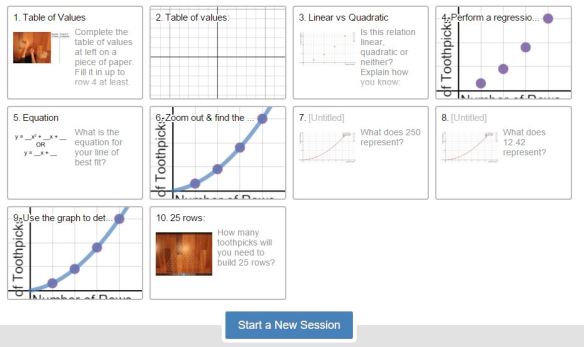Instead of the typical handout I’ve used in the past to consolidate these sorts of activities, I created a Desmos Activity version which you can find (& use) here:This was their homework after the toothpick task.

On day 2, we used this handout to work on describing the steps in some of our solutions:
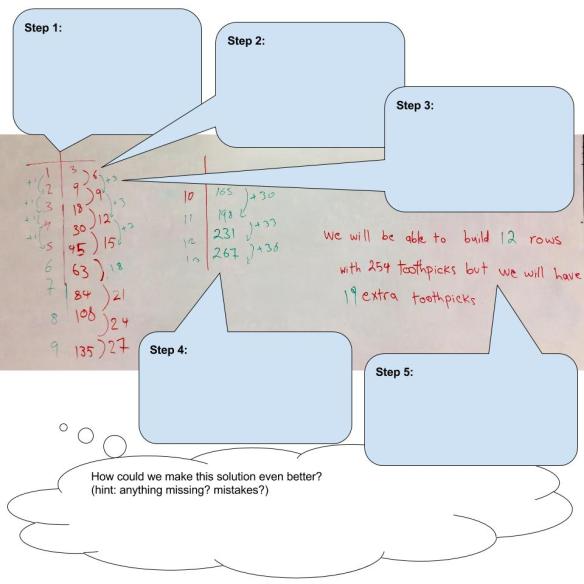Student solution:Desmos solution (which I created):

As always, all materials for this activity can be found here.

– Laura Wheeler (Teacher @ Ridgemont High School, OCDSB; Ottawa, ON)

Toothpick Houses

Here is the 3 act math task we did in my MFM2P class today:

2 of the 5 groups found a rule (albeit two different rules) to calculate higher values like 500 houses. One group (on the chalkboard) found the rule I was expecting using slope & y-intercept of 4 x step number + 1. The group on the whiteboard above used 5 x step number – (step number – 1) even though they didn’t write it out in that fashion. I had them explain that to me orally (which required some prodding & questioning from me to get it out of them). I love that the group came up with this 2nd rule as it wasn’t one I predicted; so awesome when they surprise me & see patterns in a new or different way from me!

Mostly all of the groups counted up in pictures or tables to solve for 30 houses. Note to self: pick a higher number next time, maybe 99?

Here they are making a row of 30 houses to check their answer (act 3):

– Laura Wheeler (Teacher @ Ridgemont High School, OCDSB; Ottawa, ON