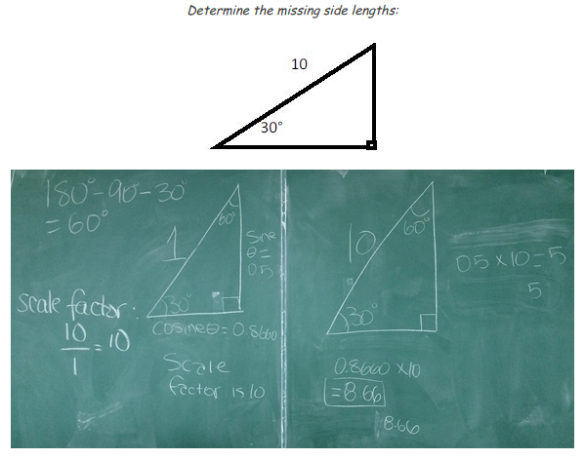
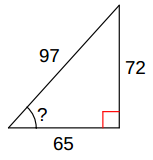
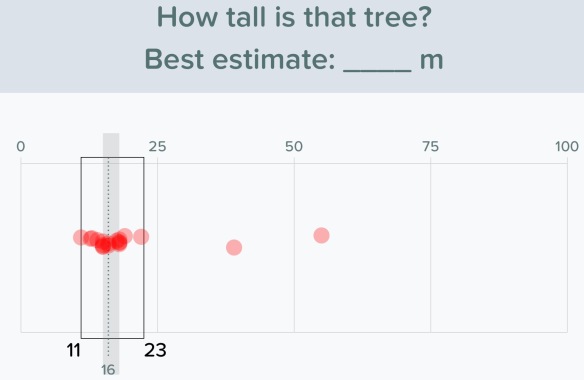
I had the pleasure of welcoming Peter Liljedahl to visit my classroom this past week. Peter is the brains behind the Thinking Classroom framework that I’ve been implementing in my classroom over the last few years. While he was in town this week for the OAME Leadership conference he took the time to visit some Thinking Classrooms in the area and I was lucky enough to have him come visit ours. He spent a period with my grade 10 applied students where I was running a problem-based learning task (or 3 Act Math task) to do with solving for the missing angle in a right triangle.

Peter Liljedahl & Judy Larsen visit
The two most popular elements that most people know about Peter’s Thinking Classroom framework are vertical non-permanent surfaces and visibly random groups. Another of the elements is to have students take meaningful notes after the problem-solving task; giving them time to select, organize & synthesize the ideas they want to keep in their notes. My way of doing this has been to create course packs for each of the courses I teach. Peter shared out this idea during his keynote on Friday and a number of teachers were interested in hearing more about them and seeing examples, so I figure a blog post was in order!
What are my course packs?
They are approximately 10 pages long (1 page per overall expectation for the course) or 5 sheets back to back. There is a box for each of the key terms or skills they need to know (I pull these from the specific expectations listed in the curriculum docs). For my applied classes I usually fill it in with worked examples of the skills, but leave the key terms blank for them to complete (see below right). For my academic classes I usually leave every box blank for students to complete (see below left). I copy & staple one for each student and hand it out at the beginning of the course.
How do we use them?
A place for meaningful notes: After each activity we do, I get my students to take out their course pack & open to whichever page matches the content we covered that day. I give them time to write their own notes based on the student work on the boards, the short notes I may have written on a board or on their boards, and I’ve also suggested mathisfun.com as a good site for definitions at their level. I also encourage them to put both images & words in every box.
A reference document: When groups go up to their boards to solve the day’s problem, one of the 3 members is given the role of bringing the course pack (the other 2 are responsible for scribing and calculating, respectively). Groups will often look through the worked examples if they need some help solving the day’s problem or remembering how to do something. On individual practice days, students often have their course pack out to help them with their practice problems. When students are stuck on a problem, I’ll often ask them to show me where a similar problem is in their course pack & we’ll use that as our starting point as we work together.
Can I see some examples?
Sure can!
Grade 10 applied course pack
Destreamed grade 9 (applied & academic together) course pack:
Grade 10 academic course notes
Still have some questions? Hit me up in the comments below or on Twitter! Have you made some of your own? Share links to your course packs below too!
– Laura Wheeler (Teacher @ Ridgemont High School, OCDSB; Ottawa, ON)









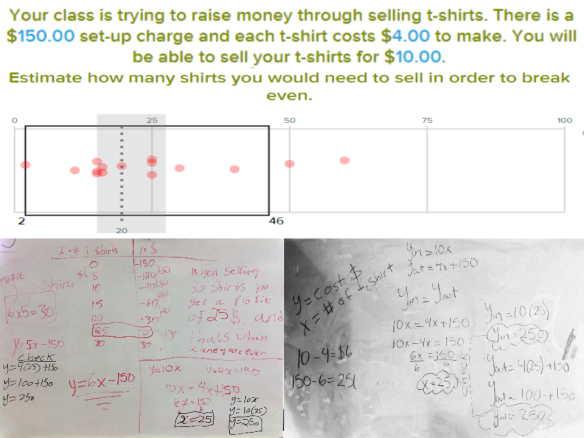
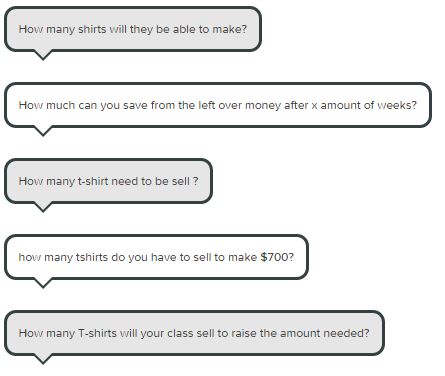




 I’m trying to blog more about my lessons/activities/problems this year. Today’s is more of a problem-based learning approach I guess. My goal was to review solving systems graphically with my grade 10 academic students.
I’m trying to blog more about my lessons/activities/problems this year. Today’s is more of a problem-based learning approach I guess. My goal was to review solving systems graphically with my grade 10 academic students.
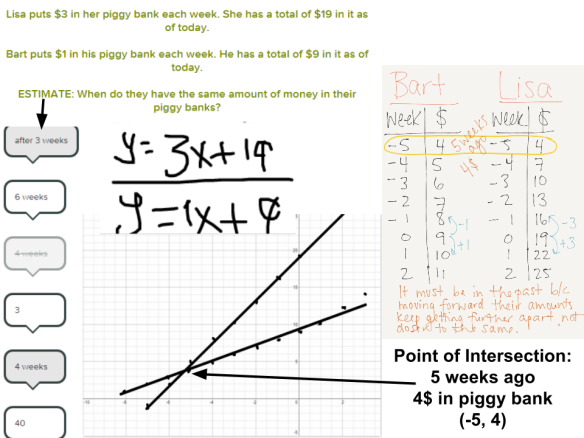
 For my MFM2P group this followed the
For my MFM2P group this followed the 

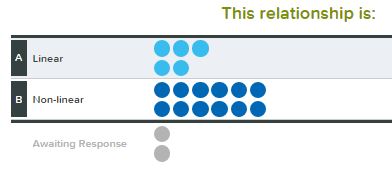
 We then discussed the shape of the graph being a curved line & the first differences being not equal (which only some students had pointed out).
We then discussed the shape of the graph being a curved line & the first differences being not equal (which only some students had pointed out).

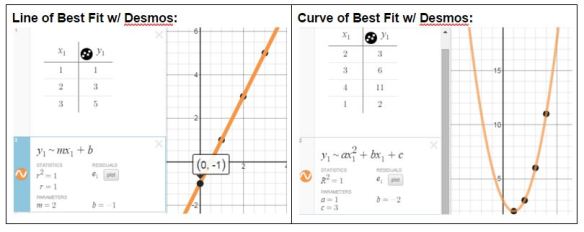 The 2P students had practiced performing a linear regression with Desmos the day before during the Perimeter investigation. The 2D students had mostly never seen Desmos before. I walked around helping students that got stuck or couldn’t find where they’d mistyped something & gotten an error. The result was:
The 2P students had practiced performing a linear regression with Desmos the day before during the Perimeter investigation. The 2D students had mostly never seen Desmos before. I walked around helping students that got stuck or couldn’t find where they’d mistyped something & gotten an error. The result was: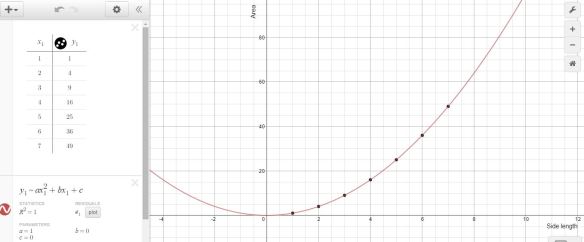 at which point I did some direct teaching about how to use the a, b, and c value determined by Desmos to write out an equation for the relationship between side length and area. I also introduced the word parabola to them while we looked at the graph from Desmos, zooming in & out.
at which point I did some direct teaching about how to use the a, b, and c value determined by Desmos to write out an equation for the relationship between side length and area. I also introduced the word parabola to them while we looked at the graph from Desmos, zooming in & out. and this became the homework for the MFM2P class as we ran out of time in class.
and this became the homework for the MFM2P class as we ran out of time in class.